Previously, I introduced a problem I was trying to solve where a large datastructure was being pinned into memory for occasional lookups. This post delves into the implemented solution which pushes it onto disk but retains (relatively) fast lookups. I think using a database or a B-Tree is a good solution to this kind of problem in general, but it was fun and inexpensive to implement this utility, and it turned out to be generally useful. Bear with me if you already understand HashMaps pretty well, because I'm basically describing a HashMap here, but it's a disk-based HashMap.

Logically, the data consists of a series of key-value pairs. The keys and values are of variable size, because they contain strings. If we were to write only the values to disk in a binary format, we might have something like this for the JSON example in the previous post:

There are two records, at offsets 0x00000000 and 0x000000A4. If we had some way to map a key to one of these offsets, we could seek() to that offset on disk and read a single record. We'll need some kind of index for that. A simple thing we could do is to store a table of the hashCode() of each key to the offset of the value. The hashcodes are as follows:

• //src/com/foo/bar/baz:baz ⟶ -691376290 (0xD6CA6F5E)
• //foo/far/fun:fun ⟶ -1488203677 (0xA74BD063)

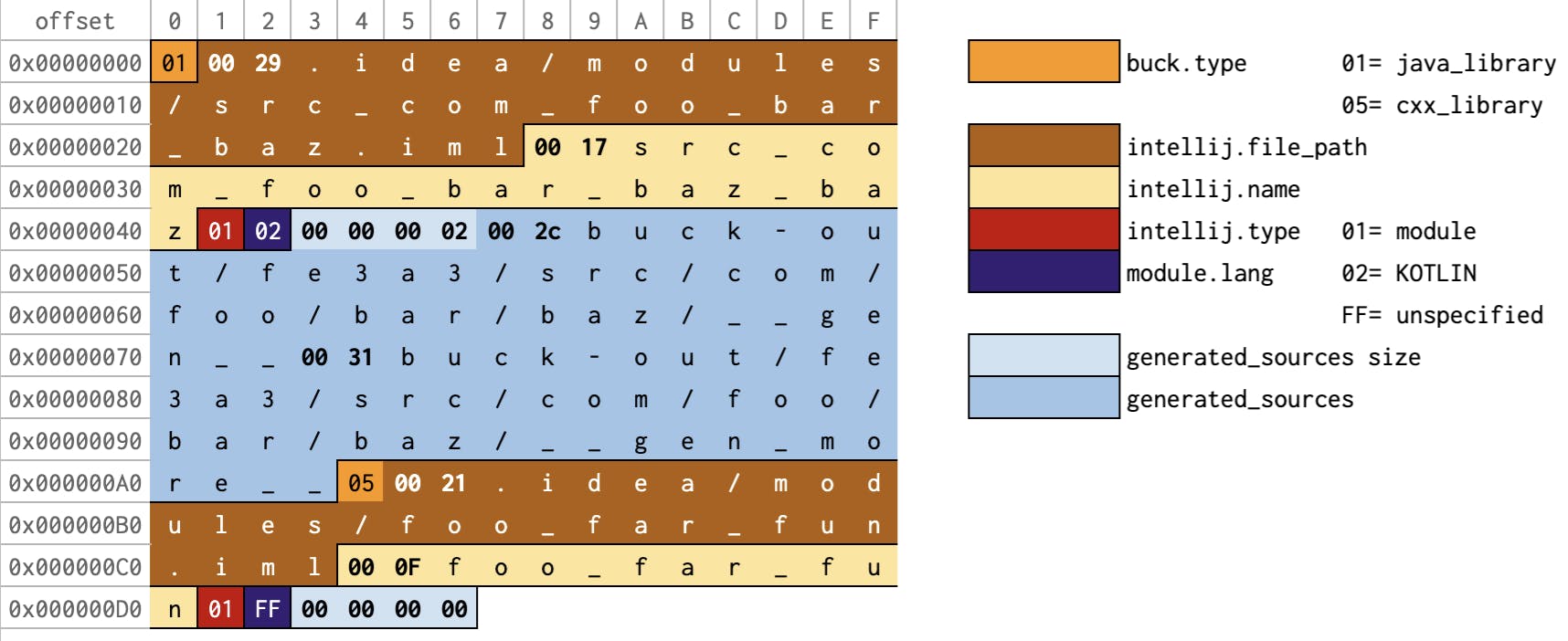
So, our index is a simple table that looks like the diagram below. Notice that we've added 0x10 to the offsets because the index is at the start of the file and is 0x10 bytes long, pushing the values down by that much (also, in the real implementation, the offsets are longs, but I made them ints to keep this diagram and example more readable :)).

We store the index sorted by the hashcode. Given a key to look up, we can then compute its hashcode and use binary search in the index portion of the file to easily find an offset. This requires O(log n) seeks over the index, followed by a single seek to the position of the record.

We could also have stored this in a more conventional hashmap style by calculating the modulus of the hashcode with some known index size, or computing a perfect hash. However, I'm always looking for a random excuse to write binary search again :)

With this scheme, there's still the possibility that a hashcode will match for two keys, so we actually store a list of records at each offset, along with their keys so we can disambiguate. In practice, in our real dataset, there happen to be zero collisions at present, so this is a bit wasteful. Again, should really use a perfect hash.

This datastructure is completely impractical if we want to support insertion, because we'd have to push the entire value set down in the file. In practice, we always just write the entire file each time (it takes about 250ms for the data we have), which neatly side steps this problem. If insertion were desirable, separating the index and data into two separate files would probably be a better approach, so the data could just be appended to the values file. You'd probably rewrite the index each time because it's sorted, but the index is much smaller than the values data anyway (in our case, it's a little over 1MB with 100,000 entries - 12 bytes per entry, and it could probably be 8 bytes per entry if we used int rather than long offsets).

Performance

The performance of a single key lookup with this is approximately _disk_seek_time + (log n * disk_seek_time) + record_read_time_. For a SSD with seek time of 0.10ms and 100,000 entries, we'd expect a lookup to take around 2-3ms. This is an upper bound of the performance I see experimentally from the implementation. It'd be far worse on a spinning disk, but our developers don't have those. The memory cost is O(1), a fancy way of just saying that we don't need to load the whole blimmin' map into memory like we were before.

Implementation

As it happens, this whole thing was implemented as part of Buck, which is opensource. So if you're interested, you can find the source code in GitHub. The main implementation is in HashFile.java - it's pretty simple (less than 200 lines of code). You can find some unit tests that show off usage of it in HashFileTest.java. Enjoy!